Duyệt cây nhị phân tìm kiếm
Trong bài viết này, codehow sẽ hướng dẫn các bạn cách để duyệt cây nhị phân tìm kiếm. Đối với cây nhị phân tìm kiếm ta có rất nhiều cách để duyệt cây, mỗi cách sẽ cho chúng ta một kết quả khác nhau.
Các cách để duyệt cây nhị phân tìm kiếm bao gồm:
- Duyệt NLR (Node - Left - Right) cây nhị phân tìm kiếm.
- Duyệt NRL (Node - Right - Left) cây nhị phân tìm kiếm.
- Duyệt LNR (Left - Node - Right) cây nhị phân tìm kiếm.
- Duyệt RNL (Right - Node - Left) cây nhị phân tìm kiếm.
- Duyệt LRN (Left - Right - Node) cây nhị phân tìm kiếm.
- Duyệt RLN (Right - Left - Node) cây nhị phân tìm kiếm.
Về cơ bản thì các cách duyệt này đều thực hiện tương tự nhau, chỉ khác thứ tự duyệt. Vậy nên mình sẽ lấy một cách duyệt làm mình họa, trong cách này mình sẽ giải thích chi tiết cách duyệt node. đối với các cách còn lại mình sẽ đưa ra hàm duyệt, các bạn có thể tự chạy bằng tay nhé.
Bây giờ các bạn cùng mình đi tìm hiểu từng cách duyệt cây nhị phân tìm kiếm thôi nào.
Duyệt NLR cây nhị phân tìm kiếm
Giả sử mình có một cây bao gồm các số sau đây: 5, 1, 2, -2, 6, 7. Sau khi thêm lần lượt các node vào cây ta được cây như hình dưới đây.
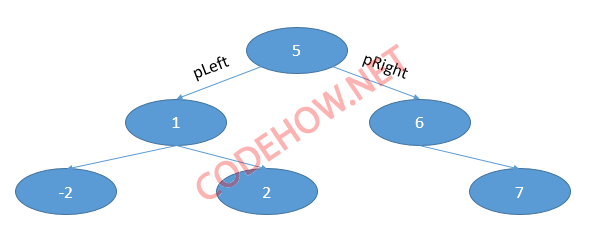
Đối với cách duyệt NLR nghĩa là chúng ta sẽ duyệt node trước, rồi đến Left rồi đến Right. Bâu giờ mình sẽ duyệt từng bước một cho các bạn xem nhé.
Bước 1: Duyệt node 5, theo quy tắc NLR thì ta sẽ xuất node 5 rồi thực hiện duyệt Left.
Bước 2: Khi duyệt Left ta lại có một node mới là 1, theo quy tắc LNR ta lại xuất node 1 ra rồi thực hiện duyệt Left.
Bước 3: Khi duyệt Left ta lại có node mới là -2, theo quy tắc LNR ta lại xuất node -2 rồi thực hiện duyệt Left. Lúc này Left không còn node nào nên sẽ chuyển qua duyệt Right. Right cũng không có node nào nên sẽ gọi đệ quy để quay lại bước 2 để thực hiện duyệt Right node 1.
Bước 4: Duyệt Right node 1 ta có node 2, theo quy tắc NLR thì ta xuất node 2 rồi thực hiện duyệt Left. Tuy nhiên Left không còn node và Right cũng vậy, nên ta sẽ gọi đệ quy để quay lại bước 1 để duyệt Right node 5.
Bước 5: Cứ như vậy ta lại duyệt Right node 6 và 7 rồi xuất ra màn hình.
Sau khi kết thúc theo cách duyệt NLR ra được danh sách các node bao gồm 5, 1, -2, 2, 6, 7. Danh sách này khác với danh sách ban đầu chúng ta thêm vào cây nhị phân tìm kiếm.
Hàm duyệt NLR cây nhị phân tìm kiếm:
/* hàm xuất cây nhị phân theo NLR */
void Duyet_NLR(TREE t)
{
// nếu cây còn phần tử thì tiếp tục duyệt
if (t != NULL)
{
cout << t->data << " "; // xuất dữ liệu trong node
Duyet_NLR(t->pLeft); // duyệt qua trái
Duyet_NLR(t->pRight); // duyệt qua phải
}
}Kết quả:
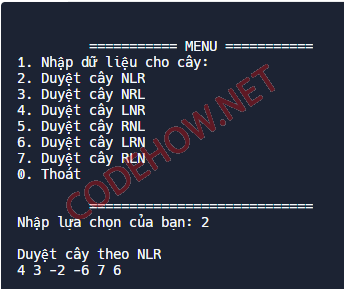
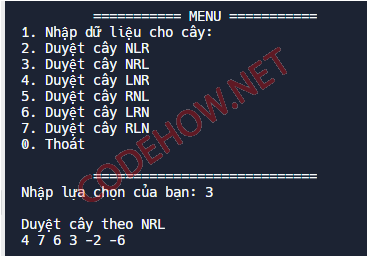
Duyệt NRL cây nhị phân tìm kiếm
Với dãy số 5, 1, 2, -2, 6, 7 khi thực hiện duyệt theo cách NRL ra sẽ được kết quả 5, 6, 7, 1, 2, -2.
Hàm duyệt NRL cây nhị phân tìm kiếm:
// hàm xuất cây nhị phân theo NRL
void Duyet_NRL(TREE t)
{
// nếu cây còn phần tử thì tiếp tục duyệt
if (t != NULL)
{
cout << t->data << " "; // xuất dữ liệu trong node
Duyet_NRL(t->pRight); // duyệt qua phải
Duyet_NRL(t->pLeft); // duyệt qua trái
}
}Kết quả:
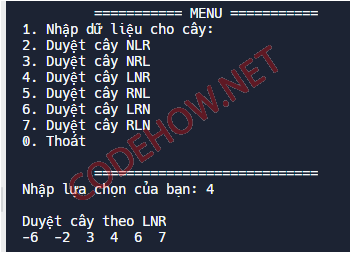
Duyệt LNR cây nhị phân tìm kiếm (tăng dần)
Đối với cách duyệt LNR cây nhị phân tìm kiếm, sau khi duyệt kết quả sẽ tằng dần.
Hàm duyệt LNR cây nhị phân tìm kiếm.
// hàm xuất cây nhị phân theo LNR <=> xuất ra các phần tử từ bé đến lớn
void Duyet_LNR(TREE t)
{
// nếu cây còn phần tử thì tiếp tục duyệt
if (t != NULL)
{
Duyet_LNR(t->pLeft); // duyệt qua trái
cout << t->data << " "; // xuất giá trị của node
Duyet_LNR(t->pRight); // duyệt qua phải
}
}Kết quả:
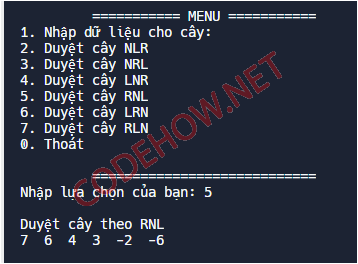
Duyệt RNL cây nhị phân tìm kiếm (giảm dần)
Đối với cách duyệt RNL cây nhị phân tìm kiếm ta sẽ được kết quả là một danh sách giảm dần.
Hàm duyệt RNL cây nhị phân tìm kiếm.
// hàm xuất cây nhị phân theo RNL <=> xuất ra các phần tử từ lớn đến bé
void Duyet_RNL(TREE t)
{
// nếu cây còn phần tử thì tiếp tục duyệt
if (t != NULL)
{
Duyet_RNL(t->pRight); // duyệt qua phải
cout << t->data << " "; // xuất giá trị của node
Duyet_RNL(t->pLeft); // duyệt qua phải
}
}Kết quả:
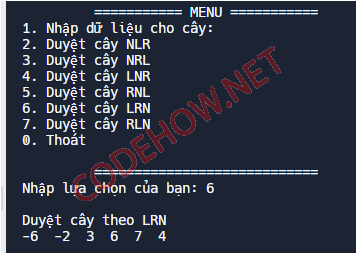
Duyệt LRN cây nhị phân tìm kiếm
Duyệt LRN cây nhị phân tìm kiếm sẽ duyệt theo thứ tự Left - Right - Node.
Hàm duyệt LRN cây nhị phân tìm kiếm.
// hàm xuất cây nhị phân theo LRN
void Duyet_LRN(TREE t)
{
// nếu cây còn phần tử thì tiếp tục duyệt
if (t != NULL)
{
Duyet_LRN(t->pLeft); // duyệt qua trái
Duyet_LRN(t->pRight); // duyệt qua phải
cout << t->data << " "; // xuất giá trị của node
}
}Kết quả:
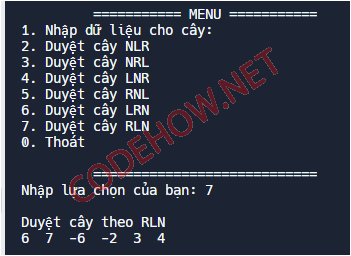
Duyệt RLN cây nhị phân tìm kiếm
Cà cuối cùng là duyệt RLN cây nhị phân tìm kiếm, đối với cách này ta sẽ duyệt theo thứ tự Right - Light - Node.
Hàm duyệt RLN cây nhị phân tìm kiếm.
// hàm xuất cây nhị phân theo RLN
void Duyet_RLN(TREE t)
{
// nếu cây còn phần tử thì tiếp tục duyệt
if (t != NULL)
{
Duyet_RLN(t->pRight); // duyệt qua phải
Duyet_RLN(t->pLeft); // duyệt qua trái
cout << t->data << " "; // xuất giá trị của node
}
}Kết quả:
Ví dụ duyệt cây nhị phân tìm kiếm
Trong phần này mình sẽ thực hiện chương trình duyệt cây nhị phân theo các cách đã nêu ở trên. Mình sẽ tạo một menu với các cách duyệt khác nhau, các bạn chỉ cần lựa chọn để duyệt cây nhị phân tìm kiếm như mình mong muốn.
Chương trình được viết bằng ngôn ngữ C++, các bạn có thể tham khảo nhé.
#include<iostream>
using namespace std;
// khai báo cấu trúc 1 cái node
struct node
{
int data; // dữ liệu của node ==> dữ liệu mà node sẽ lưu trữ
struct node *pLeft; // node liên kết bên trái của cây <=> cây con trái
struct node *pRight; // node liên kết bên phải của cây <=> cây con phải
};
typedef struct node NODE;
typedef NODE* TREE;
// khởi tạo cây
void KhoiTaoCay(TREE &t)
{
t = NULL; // cây rỗng
}
// hàm thêm phần tử x vào cây nhị phân
void ThemNodeVaoCay(TREE &t, int x)
{
// nếu cây rỗng
if (t == NULL)
{
NODE *p = new NODE; // khởi tạo 1 cái node để thêm vào cây
p->data = x;// thêm dữ liệu x vào data
p->pLeft = NULL;
p->pRight = NULL;
t = p;// node p chính là node gốc <=> x chính là node gốc
}
else // cây có tồn tại phần tử
{
// nếu phần tử thêm vào mà nhỏ hơn node gốc ==> thêm nó vào bên trái
if (t->data > x)
{
ThemNodeVaoCay(t->pLeft, x); // duyệt qua trái để thêm phần tử x
}
else if (t->data < x) // nếu phần tử thêm vào mà lớn hơn node gốc ==> thêm nó vào bên phải
{
ThemNodeVaoCay(t->pRight, x); // duyệt qua phải để thêm phần tử x
}
}
}
// hàm xuất cây nhị phân theo NLR
void Duyet_NLR(TREE t)
{
// nếu cây còn phần tử thì tiếp tục duyệt
if (t != NULL)
{
cout << t->data << " "; // xuất dữ liệu trong node
Duyet_NLR(t->pLeft); // duyệt qua trái
Duyet_NLR(t->pRight); // duyệt qua phải
}
}
// hàm xuất cây nhị phân theo NRL
void Duyet_NRL(TREE t)
{
// nếu cây còn phần tử thì tiếp tục duyệt
if (t != NULL)
{
cout << t->data << " "; // xuất dữ liệu trong node
Duyet_NRL(t->pRight); // duyệt qua phải
Duyet_NRL(t->pLeft); // duyệt qua trái
}
}
// hàm xuất cây nhị phân theo LNR <=> xuất ra các phần tử từ bé đến lớn
void Duyet_LNR(TREE t)
{
// nếu cây còn phần tử thì tiếp tục duyệt
if (t != NULL)
{
Duyet_LNR(t->pLeft); // duyệt qua trái
cout << t->data << " "; // xuất giá trị của node
Duyet_LNR(t->pRight); // duyệt qua phải
}
}
// hàm xuất cây nhị phân theo RNL <=> xuất ra các phần tử từ lớn đến bé
void Duyet_RNL(TREE t)
{
// nếu cây còn phần tử thì tiếp tục duyệt
if (t != NULL)
{
Duyet_RNL(t->pRight); // duyệt qua phải
cout << t->data << " "; // xuất giá trị của node
Duyet_RNL(t->pLeft); // duyệt qua phải
}
}
// hàm xuất cây nhị phân theo LRN
void Duyet_LRN(TREE t)
{
// nếu cây còn phần tử thì tiếp tục duyệt
if (t != NULL)
{
Duyet_LRN(t->pLeft); // duyệt qua trái
Duyet_LRN(t->pRight); // duyệt qua phải
cout << t->data << " "; // xuất giá trị của node
}
}
// hàm xuất cây nhị phân theo RLN
void Duyet_RLN(TREE t)
{
// nếu cây còn phần tử thì tiếp tục duyệt
if (t != NULL)
{
Duyet_RLN(t->pRight); // duyệt qua phải
Duyet_RLN(t->pLeft); // duyệt qua trái
cout << t->data << " "; // xuất giá trị của node
}
}
// hàm nhập dữ liệu
void Menu(TREE &t)
{
while (true)
{
cout << "\n\n\t\t =========== MENU ===========";
cout << "\n1. Nhập dữ liệu cho cây: ";
cout << "\n2. Duyệt cây NLR";
cout << "\n3. Duyệt cây NRL";
cout << "\n4. Duyệt cây LNR";
cout << "\n5. Duyệt cây RNL";
cout << "\n6. Duyệt cây LRN";
cout << "\n7. Duyệt cây RLN";
cout << "\n0. Thoát";
cout << "\n\n\t\t ============================";
int luachon;
cout << "\nNhập lựa chọn của bạn: ";
cin >> luachon;
if (luachon < 0 || luachon > 7)
{
cout << "\nLựa chọn không hợp lệ";
}
else if (luachon == 1)
{
int x;
cout << "\nNhập số nguyên x: ";
cin >> x;
ThemNodeVaoCay(t, x);
}
else if (luachon == 2)
{
cout << "\nDuyệt cây theo NLR\n";
Duyet_NLR(t);
}
else if (luachon == 3)
{
cout << "\nDuyệt cây theo NRL\n";
Duyet_NRL(t);
}
else if (luachon == 4)
{
cout << "\nDuyệt cây theo LNR\n";
Duyet_LNR(t);
}
else if (luachon == 5)
{
cout << "\nDuyệt cây theo RNL\n";
Duyet_RNL(t);
}
else if (luachon == 6)
{
cout << "\nDuyệt cây theo LRN\n";
Duyet_LRN(t);
}
else if (luachon == 7)
{
cout << "\nDuyệt cây theo RLN\n";
Duyet_RLN(t);
}
else
{
break;
}
}
}
int main()
{
TREE t;
KhoiTaoCay(t);
Menu(t);
cout<<"\n-------------------------------------\n";
cout<<"Chương trình này được đăng tại codehow.net";
}Như vậy là chúng ta đã cùng nhau tìm hiểu về các cách duyệt cây nhị phân tìm kiếm. Ở bài viết tiếp theo mình sẽ hướng dẫn các bạn cách tìm kiếm trên cây nhị phân. Đây là một thao tác đặc biệt của cây nhị phân, bởi vì thao tác này mà cây có tên là cây nhị phân tìm kiếm. Các bạn chú ý theo dõi nhé, cảm ơn các bạn rất nhiều!!!

 Giải phương trình bậc nhất ax + b = 0 trong C / C++
Giải phương trình bậc nhất ax + b = 0 trong C / C++  Lệnh Alert trong Javascript
Lệnh Alert trong Javascript 