Xuất node con và node lá trong cây nhị phân tìm kiếm
Trong bài viết này, codehow sẽ hướng dẫn các bạn cách xuất node con và node lá trong cây nhị phân tìm kiếm. Trước khi đi vào bài này, các bạn cần tìm hiểu node con và node lá là gì đã nhé.
Trong cây nhị phân tìm kiếm, node có một con là node mà bên dưới nó chỉ có một node con duy nhất. Node có hai con có node bến dưới nó có hai con nằm bên trái và bên phải. Node lá là node không chứa node con nào cả. Các bạn có thể xem hình dưới đây.
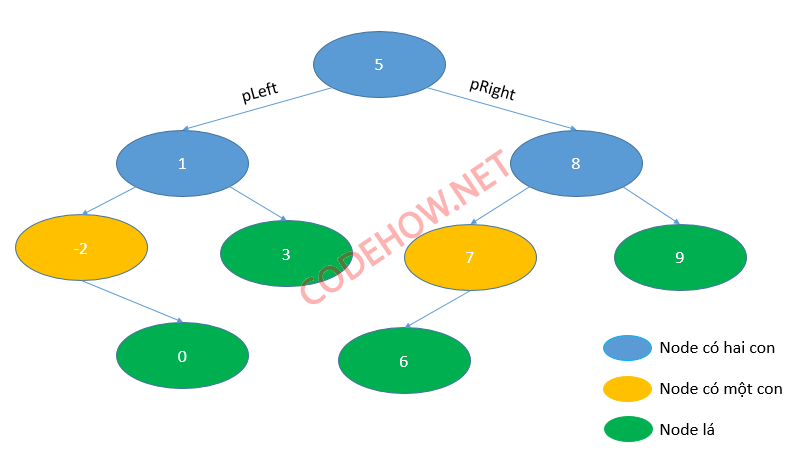
Vậy làm thế nào để có thể xuất các node con và node lá trong cây nhị phân, các bạn cùng mình lần lượt tìm hiểu thôi nhé.
Xuất các node có hai node con trong cây nhị phân tìm kiếm
Node có hai node con nghĩa là bên trái và bên phải của nó sẽ có node con. Ví dụ như hình dưới đây:
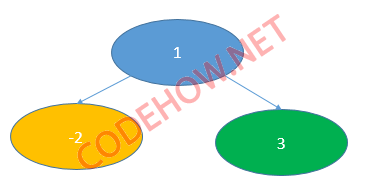
Trong hình trên, node số 1 có màu xanh dương là node có hai node con. Con của nó là hai node -2 và 3.
Các bạn hãy xem hàm xuất node có hai con node trong cây nhị phân tìm kiếm dưới đây, sau đó mình sẽ giải thích ngay bên dưới nhé.
// xuất các node có 2 con
void Node_Co_2_Con(TREE t)
{
if (t != NULL)
{
// xử lí
if (t->pLeft != NULL && t->pRight != NULL) // con trái và con phải có tồn tại phần tử
{
cout << t->data << " ";
}
Node_Co_2_Con(t->pLeft); // duyệt sang cây con trái của node hiện tại
Node_Co_2_Con(t->pRight); // duyệt sang cây con phải của node hiện tại
}
}Giải thích:
- Đầu tiên chúng ta cần kiểm tra xem cây có rỗng không nhé, nếu rỗng thì chúc ta thoát khỏi hàm nhé.
- Trong trường hợp cây có chưa phần tử, ta kiểm tra cây con bên trái và cây con bên phải. Nếu cả hai đều khác NULL thì đây chính là node có chứa hai node con.
- Sau khi kiểm tra xong, ta gọi đệ quy để tiếp túc duyệt qua cây con bên trái và bên phải cho đến khi hết cây,
Xuất các node có một node con trong cây nhị phân tìm kiếm
Một node mà có chưa một node con ngay bên dưới nó được gọi là node có chữa một node con. Ví dụ như hình dưới đây:
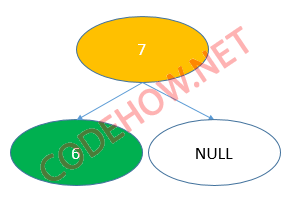
Trong hình trêm, node 7 là node có chứa một node con bên trái là node 6 và bên phải chứa NULL. Một node mà chỉ chứa mỗi node con bên trái hoặc bên phải thì được gọi là node có chứa một node con.
Đối với trường hợp này, ta chỉ cần thay đổi một chút điều kiện từ hàm xuất node có chứa hai node con là xong. Cụ thể như sau:
- Ta kiểm tra hai trường hợp nếu node bên trái có chứa node con và bên phải NULL hoặc bên trái NULL và bên phải chứa node con.
- Sau đó gọi đệ quy để duyệt sang cây con bên trái và cây con bên phải để tiêp tục xuất các node chứa một node con.
// xuất các node có 1 con
void Node_Co_1_Con(TREE t)
{
if (t != NULL)
{
// xử lí
if ((t->pLeft != NULL && t->pRight == NULL) || (t->pLeft == NULL && t->pRight != NULL))
{
cout << t->data << " ";
}
Node_Co_1_Con(t->pLeft); // duyệt sang cây con trái của node hiện tại
Node_Co_1_Con(t->pRight); // duyệt sang cây con phải của node hiện tại
}
}Xuất các node lá trong cây nhị phân tìm kiếm
Đối với trường hợp này khá đặt biệt, node lá là node mà cả bên trái và bên phải đều không chứa node con nào. Như vậy ta chỉ cần kiểm tra nếu node con bên trái và bên phải bằng NULL thì đây chính là node lá.
Sau đó gọi đệ quy để duyệt sang cây con bên trái và cây con bên phải cho đến khi hết cây nhé.
// xuất các node lá
void Node_La(TREE t)
{
if (t != NULL)
{
// xử lí
if (t->pLeft == NULL && t->pRight == NULL)
{
cout << t->data << " ";
}
Node_La(t->pLeft); // duyệt sang cây con trái của node hiện tại
Node_La(t->pRight); // duyệt sang cây con phải của node hiện tại
}
}Ví dụ xuất các node con và node lá trong cây nhị phân tìm kiếm
Trong phần này mình sẽ thực hiện một chương trình xuất các node con và node lá trong cây nhị phân. Cụ thể các yêu cầu như sau:
- Xây dựng cấu trúc cây nhị phân tìm kiếm và cấu trúc node.
- Tạo hàm thêm node vào cây.
- Tạo hàm duyệt cây.
- Tạo hàm xuất node có hai node con.
- Tạo hàm xuất node có một node con.
- Tạo hàm xuất node lá.
- Tạo menu bao gồm các yêu cầu trên cho người dùng lựa chọn.
Bây giờ chúng ta sẽ đi thực hiện từng yêu cầu nhé.
Bước 1: Xây dựng cấu trúc cây nhị phân tìm kiếm và cấu trúc node.
// khai báo cấu trúc 1 cái node trong cây nhị phân tìm kiếm
struct node
{
int data; // dữ liệu chứa trong 1 cái node
struct node *pLeft; // con trỏ liên kết với cái node bên trái <=> cây con trái
struct node *pRight; // con trỏ liên kết với cái node bên phải <=> cây con phải
};
typedef struct node NODE;
typedef NODE* TREE;
// hàm khởi tạo cây nhị phân tìm kiếm
void KhoiTaoCay(TREE &t)
{
t = NULL;
}Bước 2: Tạo hàm thêm node vào cây.
// hàm thêm 1 cái phần tử vào cây
void ThemNodeVaoCay(TREE &t, int x)
{
// nếu cây rỗng
if (t == NULL)
{
NODE *p = new NODE;
p->data = x;
p->pLeft = NULL;
p->pRight = NULL;
t = p;
}
else
{
// nếu phần tử thêm vào mà nhỏ hơn nút gốc thì sẽ duyệt qua bên trái
if (x < t->data)
{
ThemNodeVaoCay(t->pLeft, x);
}
else if (x > t->data)
{
ThemNodeVaoCay(t->pRight, x);
}
}
}Bước 3: Tạo hàm duyệt cây.
// hàm xuất phần tử trong cây nhị phân tìm kiếm
void NLR(TREE t)
{
if (t != NULL)
{
// xử lí
cout << t->data << " ";
NLR(t->pLeft);
NLR(t->pRight);
}
}Bước 4: Tạo hàm xuất node có hai node con.
// xuất các node có 2 con
void Node_Co_2_Con(TREE t)
{
if (t != NULL)
{
// xử lí
if (t->pLeft != NULL && t->pRight != NULL) // con trái và con phải có tồn tại phần tử
{
cout << t->data << " ";
}
Node_Co_2_Con(t->pLeft); // duyệt sang cây con trái của node hiện tại
Node_Co_2_Con(t->pRight); // duyệt sang cây con phải của node hiện tại
}
}Bước 5: Tạo hàm xuất node có một node con.
// xuất các node có 1 con
void Node_Co_1_Con(TREE t)
{
if (t != NULL)
{
// xử lí
if ((t->pLeft != NULL && t->pRight == NULL) || (t->pLeft == NULL && t->pRight != NULL))
{
cout << t->data << " ";
}
Node_Co_1_Con(t->pLeft); // duyệt sang cây con trái của node hiện tại
Node_Co_1_Con(t->pRight); // duyệt sang cây con phải của node hiện tại
}
}Bước 6: Tạo hàm xuất node lá.
// xuất các node lá
void Node_La(TREE t)
{
if (t != NULL)
{
// xử lí
if (t->pLeft == NULL && t->pRight == NULL)
{
cout << t->data << " ";
}
Node_La(t->pLeft); // duyệt sang cây con trái của node hiện tại
Node_La(t->pRight); // duyệt sang cây con phải của node hiện tại
}
}Bước 7: Tạo menu bao gồm các yêu cầu trên cho người dùng lựa chọn.
// hàm nhập cây nhị phân tìm kiếm
void Menu(TREE &t)
{
int luachon;
while(true)
{
cout << "\n\n\t\t ============ MENU ============";
cout << "\n1. Nhập phần tử cho cây";
cout << "\n2. Duyệt cây";
cout << "\n3. Node có hai con";
cout << "\n4. Node có một con";
cout << "\n5. Node lá";
cout << "\n0. Thoát";
cout << "\n\n\t\t ============= END =============";
cout << "\nNhập lựa chọn của bạn: ";
cin >> luachon;
if (luachon == 1)
{
int x;
cout << "\nNhập giá trị: ";
cin >> x;
ThemNodeVaoCay(t, x);
}
else if (luachon == 2)
{
cout << "\nCây nhị phân tìm kiếm\n";
NLR(t);
}
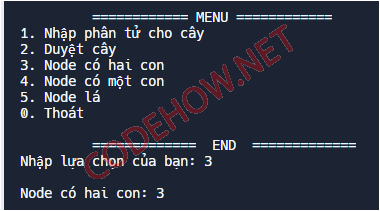
else if (luachon == 3)
{
cout << "\nNode có hai con: ";
Node_Co_2_Con(t);
}
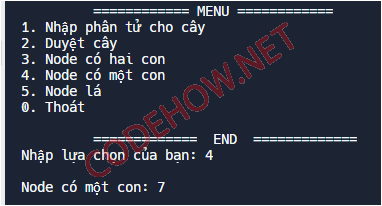
else if (luachon == 4)
{
cout << "\nNode có một con: ";
Node_Co_1_Con(t);
}
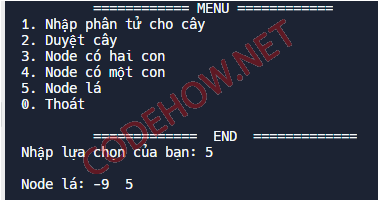
else if (luachon == 5)
{
cout << "\nNode lá: ";
Node_La(t);
}
else
{
break;
}
}
}Dưới đây là chương trình mình đã viết sẵn bằng ngôn ngữ C++, các bạn có thể tham khảo nhé.
#include<iostream>
using namespace std;
// khai báo cấu trúc 1 cái node trong cây nhị phân tìm kiếm
struct node
{
int data; // dữ liệu chứa trong 1 cái node
struct node *pLeft; // con trỏ liên kết với cái node bên trái <=> cây con trái
struct node *pRight; // con trỏ liên kết với cái node bên phải <=> cây con phải
};
typedef struct node NODE;
typedef NODE* TREE;
// hàm khởi tạo cây nhị phân tìm kiếm
void KhoiTaoCay(TREE &t)
{
t = NULL;
}
// hàm thêm 1 cái phần tử vào cây
void ThemNodeVaoCay(TREE &t, int x)
{
// nếu cây rỗng
if (t == NULL)
{
NODE *p = new NODE;
p->data = x;
p->pLeft = NULL;
p->pRight = NULL;
t = p;
}
else
{
// nếu phần tử thêm vào mà nhỏ hơn nút gốc thì sẽ duyệt qua bên trái
if (x < t->data)
{
ThemNodeVaoCay(t->pLeft, x);
}
else if (x > t->data)
{
ThemNodeVaoCay(t->pRight, x);
}
}
}
// hàm xuất phần tử trong cây nhị phân tìm kiếm
void NLR(TREE t)
{
if (t != NULL)
{
// xử lí
cout << t->data << " ";
NLR(t->pLeft);
NLR(t->pRight);
}
}
// xuất các node có 2 con
void Node_Co_2_Con(TREE t)
{
if (t != NULL)
{
// xử lí
if (t->pLeft != NULL && t->pRight != NULL) // con trái và con phải có tồn tại phần tử
{
cout << t->data << " ";
}
Node_Co_2_Con(t->pLeft); // duyệt sang cây con trái của node hiện tại
Node_Co_2_Con(t->pRight); // duyệt sang cây con phải của node hiện tại
}
}
// xuất các node có 1 con
void Node_Co_1_Con(TREE t)
{
if (t != NULL)
{
// xử lí
if ((t->pLeft != NULL && t->pRight == NULL) || (t->pLeft == NULL && t->pRight != NULL))
{
cout << t->data << " ";
}
Node_Co_1_Con(t->pLeft); // duyệt sang cây con trái của node hiện tại
Node_Co_1_Con(t->pRight); // duyệt sang cây con phải của node hiện tại
}
}
// xuất các node lá
void Node_La(TREE t)
{
if (t != NULL)
{
// xử lí
if (t->pLeft == NULL && t->pRight == NULL)
{
cout << t->data << " ";
}
Node_La(t->pLeft); // duyệt sang cây con trái của node hiện tại
Node_La(t->pRight); // duyệt sang cây con phải của node hiện tại
}
}
// hàm nhập cây nhị phân tìm kiếm
void Menu(TREE &t)
{
int luachon;
while(true)
{
cout << "\n\n\t\t ============ MENU ============";
cout << "\n1. Nhập phần tử cho cây";
cout << "\n2. Duyệt cây";
cout << "\n3. Node có hai con";
cout << "\n4. Node có một con";
cout << "\n5. Node lá";
cout << "\n0. Thoát";
cout << "\n\n\t\t ============= END =============";
cout << "\nNhập lựa chọn của bạn: ";
cin >> luachon;
if (luachon == 1)
{
int x;
cout << "\nNhập giá trị: ";
cin >> x;
ThemNodeVaoCay(t, x);
}
else if (luachon == 2)
{
cout << "\nCây nhị phân tìm kiếm\n";
NLR(t);
}
else if (luachon == 3)
{
cout << "\nNode có hai con: ";
Node_Co_2_Con(t);
}
else if (luachon == 4)
{
cout << "\nNode có một con: ";
Node_Co_1_Con(t);
}
else if (luachon == 5)
{
cout << "\nNode lá: ";
Node_La(t);
}
else
{
break;
}
}
}
int main()
{
TREE t;
KhoiTaoCay(t);
Menu(t);
cout<<"\n---------------------------------\n";
cout<<"Chương trình này được đăng tại codehow.net";
}Kết quả: Dãy số bao gồm 3, 7, -9. 5.

 Giải phương trình bậc nhất ax + b = 0 trong C / C++
Giải phương trình bậc nhất ax + b = 0 trong C / C++  Lệnh Alert trong Javascript
Lệnh Alert trong Javascript 