Đệ quy lồng (Nested Recursion) trong C / C++

Trong bài viết này, codehow sẽ giới thiệu cho các bạn một trong các hàm đệ quy tiếp theo đó là hàm đệ quy lồng (Nested Recursion) trong C / C++. Đây là một hàm đệ quy khá khó hiểu, bởi độ phức tạp nó khá cao. Tuy nhiên nếu các bạn nắm rõ cơ chế hoạt động của nó thì không quá khó.

Chúng ta sẽ cùng nhau tìm hiểu về hàm đệ quy lồng (Nested Recursion) là gì? Cơ chế hoạt động của nó. Cùng với đó là một ví dụ cụ thể sử dụng hàm đệ quy lồng (Nested Recursion) trong C / C++.

Hàm đệ quy lồng (Nested Recursion) trong C / C++ là gì?

Ví dụ: Mình có hàm đệ quy lồng dưới đây.

int ackerman(int m, int n){
  if(m == 0)
     return n + 1;
  else if(n == 0)
     return ackerman(m - 1, 1);
  else
     return ackerman(m-1, ackerman(m, n-1));
}

Như các bạn đã thấy hàm trên, khi thực hiện gọi đệ quy, tham số truyền vào chính là hàm đó. Tương tự như vậy ta gọi đó là hàm đệ quy lồng.

Cơ chế hoạt động của hàm đệ quy lồng (Nested Recursion) trong C / C++

Trong phần này, mình sẽ chỉ ra cơ chế hoạt động của hàm đệ quy lồng trong C / C++. Mình sẽ lấy một biểu thức truy hồi để làm ví dụ cho các bạn dễ hiểu nhé.

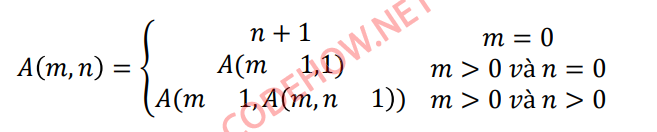
Trong phương trình trên có phần đó là kết quả trả về của phương trình và điểm dừng. Trong trường họp m > 0 và n > 0 thì tham số truyền vào là đệ quy chính nó.

Mình có hàm ackerman() để giải phương trình trên dưới đây. Vì để cho ngắn gọn, mình sẽ gọi hàm ackerman() là hàm A() nhé.

int A(int m, int n){
  if(m == 0)
    return n + 1;
  else if(n == 0)
    return A(m - 1, 1);
  else
    return A(m-1, A(m, n-1));
}

Với hàm A() mình sẽ truyền vào hai tham số m = 2 và n = 1, các bạn cùng xem cơ chế hoạt động của nó nhé.

Như các bạn thấy ở hình trên, hàm A() thực hiện gọi đệ quy rất nhiều lần và chúng lồng vào nhau. Lúc nhìn vào các bạn có thể thấy rồi, tuy nhiên nếu các bạn tuần tự thực hiện từng đệ quy một thì không khó nhé.

Các bạn có thể dựa vào đây để tự luyện tập cho mình nhé. Có thể thay đổi giá trị của m và n, sau đó ghi ra giấy hoặc đánh trên word, việc làm này giúp các bạn dễ nhớ hơn.

Bây giờ mình sẽ thực hiện viết chương trình giải phương trình truy hồi trên bằng ngôn ngữ C và C++.

Chương trình C:

#include <stdio.h>

int A(int m, int n){
  if(m == 0) // nếu m == 0 thì return n + 1
    return n + 1;
  else if(n == 0) // nếu n == 0 thì return đệ quy A(m - 1, 1)
    return A(m - 1, 1);
  else // nếu m > 0 và n > 0 thì return đệ quy lồng A(m-1, A(m, n-1))
    return A(m-1, A(m, n-1));
}
int main() {
  int kq = A(2,1); // truyển tham số đầu vào cho A() là m = 2 và n = 1
  printf("Với m = 2 và n = 1");
  printf("\nKết quả: %d",kq);
 
  printf("\n---------------------------\n");
  printf("Chương trình này được đăng tại codehow.net");
}

Chương trình C++:

#include <iostream>
using namespace std;
 
int A(int m, int n){
  if(m == 0) // nếu m == 0 thì return n + 1
    return n + 1;
  else if(n == 0) // nếu n == 0 thì return đệ quy A(m - 1, 1)
    return A(m - 1, 1);
  else // nếu m > 0 và n > 0 thì return đệ quy lồng A(m-1, A(m, n-1))
    return A(m-1, A(m, n-1));
}
int main() {
  int kq = A(2,1); // truyển tham số đầu vào cho A() là m = 2 và n = 1
  cout<<"Với m = 2 và n = 1";
  cout<<"\nKết quả: "<<kq;
 
  cout<<"\n---------------------------\n";
  cout<<"Chương trình này được đăng tại codehow.net";
}

Kết quả:

Kết luận

Như vậy là chúng ta đã cùng nhau tìm hiểu về hàm đệ quy lồng (Nested Recursion) trong C / C++. Qua bài này các bạn cần nắm các kiến thức dưới đây:

• Hàm đệ quy lồng là hàm khi gọi đệ quy và truyền tham số là một đệ quy chính nó.
• Cơ chế hoạt động của nó được thực hiện tuần tự theo các đệ quy,

Ở bài viết tiếp theo, mình sẽ giới thiệu các bạn hàm đệ quy cuối cùng trong danh sách các hàm đệ quy trong C / C++ đó là đệ quy tương hỗ. Các bạn chú ý theo dõi nhé, cảm ơn các bạn rất nhiều.