Thuật toán sắp xếp trộn (Merge Sort) trong C / C++
Trong bài viết này, codehow sẽ giới thiệu đến các bạn thuật toán sắp xếp trộn (Merge Sort) trong C / C++. Đây là một thuật toán được sử dụng khá nhiều trong lập trình, bởi tốc độ và độ chính xác của nó khá cao so với các thuật toán khác.
Trước khi vào tìm hiểu về thuật toán sắp xếp trộn (Merge Sort) trong C / C++, chúng ta hãy tìm hiểu xem sắp xếp trộn là gì? Cách thức nó hoạt động đã nhé.
Sắp xếp trộn (Merge Sort) là gì? Cách thức nó hoạt động
Thuật toán sẽ thực hiện chia mảng ban đầu thành hai nửa, rồi thực hiện sắp xếp trên từng nửa. Sau đó gộp từng nửa lại với nhau thành một mảng đã sắp xếp hoàn chỉnh.
Mình có một ví dụ minh họa dưới đây, các bạn xem để hiểu rõ hơn về cách thức hoạt động của sắp xếp trộn nhé.
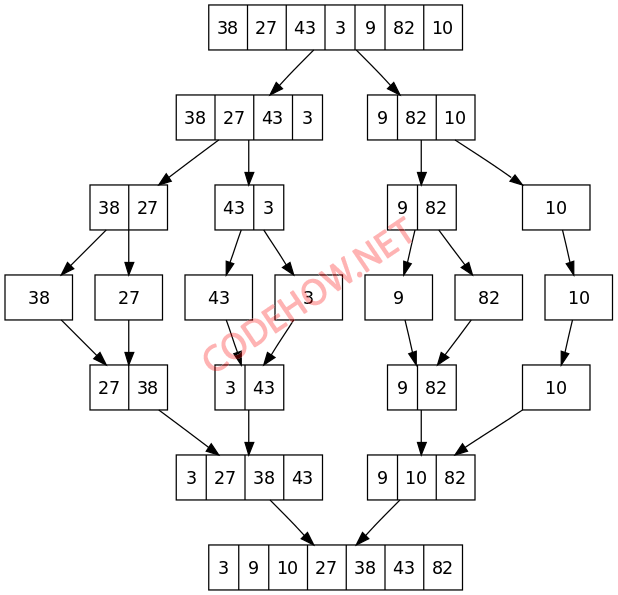
Giải thích:
- Đầu tiên thuật toán sẽ chia mảng ban đầu gồm 7 phần tử thành hai nửa mảng con, một mảng 3 phần tử và một mảng 4 phần tử.
- Tiếp tục chia nhỏ các mảng con thành hai nửa mảng con khác cho đến khi được kết quả như dòng thứ 4.
- Sau khi chia xong, bây giờ đến lúc so sánh từng phần tử nhỏ rồi gom chúng lại thành từng mảng con như dòng 5, 6, 7.
- Kết quả cuối cùng ta được mảng đã sắp xếp như dòng thứ 7 {3, 9, 10, 27, 38, 43, 82}.
Thuật toán sắp xếp trộn (Merge Sort) trong C / C++
Thuật toán sắp xếp trộn (Merge Sort) trong C / C++ được chia làm hai giai đoạn đó là chia nhỏ các phần tử và sắp xếp, gộp các phần tử lại. Như vậy chúng ta cũng sẽ tạo hai hàm để xử lý bài toán.
Hàm mergeSort():
void mergeSort(int arr[], int l, int r)
{
if (l < r)
{
int m = l+(r-l)/2;
// Gọi hàm đệ quy tiếp tục chia đôi từng nửa mảng
mergeSort(arr, l, m);
mergeSort(arr, m+1, r);
merge(arr, l, m, r);
}
}Hàm merge():
void merge(int arr[], int l, int m, int r)
{
int i, j, k;
int n1 = m - l + 1;
int n2 = r - m;
int L[n1], R[n2];//tạo 2 mảng tạm thời để chứa các phần tử sau khi chia
// Copy dữ liệu sang các mảng tạm
for (i = 0; i < n1; i++)
L[i] = arr[l + i];
for (j = 0; j < n2; j++)
R[j] = arr[m + 1+ j];
// khởi tạo các giá trị ban đầu
i = 0;
j = 0;
k = l;
//gộp hai mảng tạm thời vào mảng arr
while (i < n1 && j < n2)
{
if (L[i] <= R[j])
{
arr[k] = L[i];
i++;
}
else
{
arr[k] = R[j];
j++;
}
k++;
}
// Copy các phần tử còn lại của mảng L vào arr nếu có
while (i < n1)
{
arr[k] = L[i];
i++;
k++;
}
// Copy các phần tử còn lại của mảng R vào arr nếu có
while (j < n2)
{
arr[k] = R[j];
j++;
k++;
}
}Giải thích thuật toán:
- Trong hàm
mergeSort()ta sử dụng đệ quy để chia mảng ban đầu thành hai nửa mảng con. Cứ tiếp tục chia cho đến khi không chia được nữa. - Tạo hai mảng tạm thời để lưu các phần tử sau khi chia và hai mảng con L, R.
- Đối với trường hợp chỉ có một phần tử thì coi như đã sắp xếp.
- Sau khi đã chia xong, ta gọi hàm
merge()để gộp các phần tử ở mảng con L, R vào mảng lớn arr. - Bước cuối cùng là sắp xếp mảng đã gộp rồi tiếp tục vòng lặp tiếp theo.
Cứ như vậy cho đến khi kết thúc vòng lặp ta sẽ được một mảng đã được sắp xếp.
Dưới đây là ví dụ minh họa sử dụng thuật toán sắp xếp trộn (Merge Sort) trong C / C++. Chương trình được viết bằng hai ngôn ngữ khác nhau là C và C++, các bạn có thể tham khảo nhé.
Chương trình C:
#include <stdio.h>
#include <stdbool.h>
void merge(int arr[], int l, int m, int r)
{
int i, j, k;
int n1 = m - l + 1;
int n2 = r - m;
int L[n1], R[n2];//tạo 2 mảng tạm thời để chứa các phần tử sau khi chia
// Copy dữ liệu sang các mảng tạm
for (i = 0; i < n1; i++)
L[i] = arr[l + i];
for (j = 0; j < n2; j++)
R[j] = arr[m + 1+ j];
// khởi tạo các giá trị ban đầu
i = 0;
j = 0;
k = l;
//gộp hai mảng tạm thời vào mảng arr
while (i < n1 && j < n2)
{
if (L[i] <= R[j])
{
arr[k] = L[i];
i++;
}
else
{
arr[k] = R[j];
j++;
}
k++;
}
// Copy các phần tử còn lại của mảng L vào arr nếu có
while (i < n1)
{
arr[k] = L[i];
i++;
k++;
}
// Copy các phần tử còn lại của mảng R vào arr nếu có
while (j < n2)
{
arr[k] = R[j];
j++;
k++;
}
}
// l là chỉ số trái và r là chỉ số phải của mảng cần được sắp xếp
void mergeSort(int arr[], int l, int r)
{
if (l < r)
{
int m = l+(r-l)/2;
// Gọi hàm đệ quy tiếp tục chia đôi từng nửa mảng
mergeSort(arr, l, m);
mergeSort(arr, m+1, r);
merge(arr, l, m, r);
}
}
void printArr(int arr[], int N)
{
int i;
for (i = 0; i < N; i++)
{
printf("%d\t", arr[i]);
}
}
int main(void) {
int n;
do{
printf("\nNhập vào số lượng phần tử có trong mảng: ");
scanf("%d", &n);
}while(n <= 0);
int a[n];
for(int i = 0;i < n;i++){
printf("a[%d] = ",i);
scanf("%d",&a[i]);
};
mergeSort(a, 0, n - 1);
printf("Mảng sau khi được sắp xếp: \n");
printArr(a, n);
printf("\n---------------------------------------\n");
printf("Chương trình này được đăng tại codehow.net");
}Kết quả:
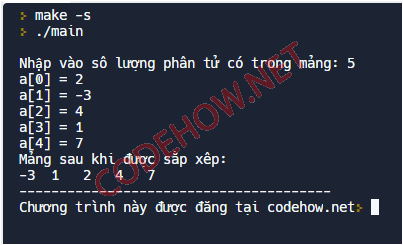
Chương trình C++:
#include <iostream>
using namespace std;
void merge(int arr[], int l, int m, int r)
{
int i, j, k;
int n1 = m - l + 1;
int n2 = r - m;
int L[n1], R[n2];//tạo 2 mảng tạm thời để chứa các phần tử sau khi chia
// Copy dữ liệu sang các mảng tạm
for (i = 0; i < n1; i++)
L[i] = arr[l + i];
for (j = 0; j < n2; j++)
R[j] = arr[m + 1+ j];
// khởi tạo các giá trị ban đầu
i = 0;
j = 0;
k = l;
//gộp hai mảng tạm thời vào mảng arr
while (i < n1 && j < n2)
{
if (L[i] <= R[j])
{
arr[k] = L[i];
i++;
}
else
{
arr[k] = R[j];
j++;
}
k++;
}
// Copy các phần tử còn lại của mảng L vào arr nếu có
while (i < n1)
{
arr[k] = L[i];
i++;
k++;
}
// Copy các phần tử còn lại của mảng R vào arr nếu có
while (j < n2)
{
arr[k] = R[j];
j++;
k++;
}
}
// l là chỉ số trái và r là chỉ số phải của mảng cần được sắp xếp
void mergeSort(int arr[], int l, int r)
{
if (l < r)
{
int m = l+(r-l)/2;
// Gọi hàm đệ quy tiếp tục chia đôi từng nửa mảng
mergeSort(arr, l, m);
mergeSort(arr, m+1, r);
merge(arr, l, m, r);
}
}
void printArr(int arr[], int N)
{
int i;
for (i = 0; i < N; i++)
{
cout<<arr[i]<<"\t";
}
}
int main(void) {
int n;
do{
cout<<"\nNhập vào số lượng phần tử có trong mảng: ";
cin>>n;
}while(n <= 0);
int a[n];
for(int i = 0;i < n;i++){
cout<<"a["<<i<<"] = ";
cin>>a[i];
};
mergeSort(a,0, n-1);
cout<<"Mảng sau khi được sắp xếp: \n";
printArr(a, n);
cout<<"\n---------------------------------------\n";
cout<<"Chương trình này được đăng tại codehow.net";
}Kết quả:
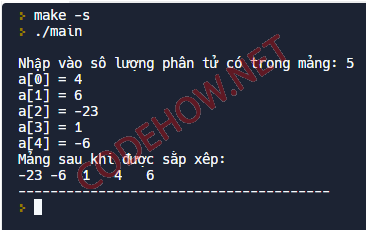
Như vậy là chúng ta đã cùng nhau tìm hiểu về thuật toán sắp xếp trộn (Merge Sort) trong C / C++. Ở bài viết tiếp theo, mình sẽ giới thiệu đến các bạn thuật toán sắp xếp nhanh, đây được coi là thuật toán sắp xếp nhanh nhất trong C / C++. Các bạn nhớ chú ý theo dõi nhé.

 Giải phương trình bậc nhất ax + b = 0 trong C / C++
Giải phương trình bậc nhất ax + b = 0 trong C / C++  Lệnh Alert trong Javascript
Lệnh Alert trong Javascript 